目录

• 爬楼梯
• 背包问题
• 热门题🔥

爬楼梯

一维爬楼梯

先从简单但最经典的开始！
70. 爬楼梯：假设你正在爬一个 n 阶的楼梯，每次可以爬 1 或 2 个台阶。有多少种不同的方法可以爬到楼顶呢？

思路：定义 dp[i] 表示爬 i+1 阶楼梯的方法总数。

• 状态转移方程：dp[i] = dp[i-1] + dp[i-2] 。
• 初始值：dp[0] = 1，dp[1] = 2 。

public int climbStairs(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    if (n == 2) return 2;

    int prev = 2;
    int sum = 3;
    for (int i = 3; i < n; i++) {
        int tmp = sum;
        sum += prev;
        prev = tmp;
    }
    return sum;

    int[] dp = new int[n];
    dp[0] = 1;
    dp[1] = 2;
    for (int i = 2; i < n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n - 1];
}

空间优化：观察到一旦算出 dp[i] ，dp[i−2] 及其左边的状态就永远不会用到了。

public int climbStairs(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    if (n == 2) return 2;

    int dp_n1 = 1;
    int dp_n2 = 1;
    for (int i = 1; i < n; i++) {
        int dp_n = dp_n1 + dp_n2;
        dp_n1 = dp_n2;
        dp_n2 = dp_n;
    }
    return dp_n2;
}

二维爬楼梯

62. 不同路径：从 m x n 网格的左上角开始，每次只能向下或者向右移动 1 步，到达网格的右下角共有多少条不同的路径？

思路：定义 dp[i][j] 表示到达网格 (i, j) 的方法总数。

• 状态转移方程：dp[i][j] = dp[i-1][j] + dp[i][j-1] 。
• 初始值：i = 0 或 j = 0 时，dp[i][j] = 0 。

public int uniquePaths(int m, int n) {
    int[][] dp = new int[m][n];
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (i == 0 || j == 0) {
                dp[i][j] = 1;
            } else {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    return dp[m - 1][n - 1];
    
    // 第一次空间优化
    int[] dp = new int[n];       // 取代 dp[i][j]
    int[] dp_prev = new int[n];  // 取代 dp[i - 1][j]
    Arrays.fill(dp_prev, 1);     // 即 i = 0 时，dp[j] = 0
    Arrays.fill(dp, 1);          // 即 j = 0 时，dp[j] = 0
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[j] = dp_prev[j] + dp[j - 1];
        }
        dp_prev = dp.clone();
    }
    return dp[n - 1];

    // 第二次空间优化
    int[] dp = new int[n];
    Arrays.fill(dp, 1);
    for (int i = 1; i < m; i++){
        for (int j = 1; j < n; j++){
            dp[j] += dp[j - 1] ;
        }
    }
    return dp[n - 1];
}

类似问题：

• 118. 杨辉三角
• 119. 杨辉三角 II

背包问题

问题描述：给定容量 target，以及一组物品的大小数组 weights，如何选取物品使得正好填满容量？

完全背包问题

每种物品可以无限次使用。

boolean[] dp = new boolean[target + 1];

dp[0] = true;

for (int weight : weights) {
    // 正序遍历，允许重复当前物品
    for (int i = weight; i <= target; i++) {
        dp[i] = dp[i] || dp[i - weight];
    }
}

return dp[target];

0/1背包问题

每种物品最多只能被选取一次。

boolean[] dp = new boolean[target + 1];

dp[0] = true;

for (int weight : weights) {
    if (weight > target) {
        break;
    }
    // 倒序遍历，确保每个物品只使用一次
    // 如果正序遍历，dp[i] 的更新会影响后续的 dp[i + weight]，导致物品被多次使用。
    for (int i = target; i > 0; i--) {
        if (i >= weight) {
            dp[i] = dp[i] || dp[i - weight];
        }
    }
}

return dp[target];

例题：

• 416. 分隔等和子集（0/1背包问题）

热门题🔥

32. 最长有效括号

问题描述：给定只包含 '(' 和 ')' 的字符串，找出最长有效且连续括号子串的长度。

• 示例 1：输入："(()" 输出：2
• 示例 2：输入：")()())" 输出：4
• 示例 3：输入："()(())" 输出：6

思路：定义 dp[i] 表示以下标 i 字符结尾的最长有效括号长度。以 '(' 结尾的子串对应的 dp 值必定为 0 ，因此我们只需讨论以 ')' 结尾的情况：

1. s[i] = ')' 且 s[i−1] = '('：此时字符串形如 "……()" 。因此 i > 1 时，有 dp[i] = dp[i−2] + 2 ；如果 i = 1 ，则 dp[i] 直接等于 2 。

2. s[i] = ')' 且 s[i−1] = ')'：此时字符串形如 "……))" 。因此去找 i 前面对应字符 prev 是否为 '(' ，其下标为 i 减去前一个字符已匹配的长度（i - dp[i-1] - 1）；如果匹配，则 dp[i] 在 dp[i-1] 的基础上加 2 ；如果 prev 前还有字符，则再加上 prev 前已匹配的长度 dp[i - dp[i-1] - 2] 。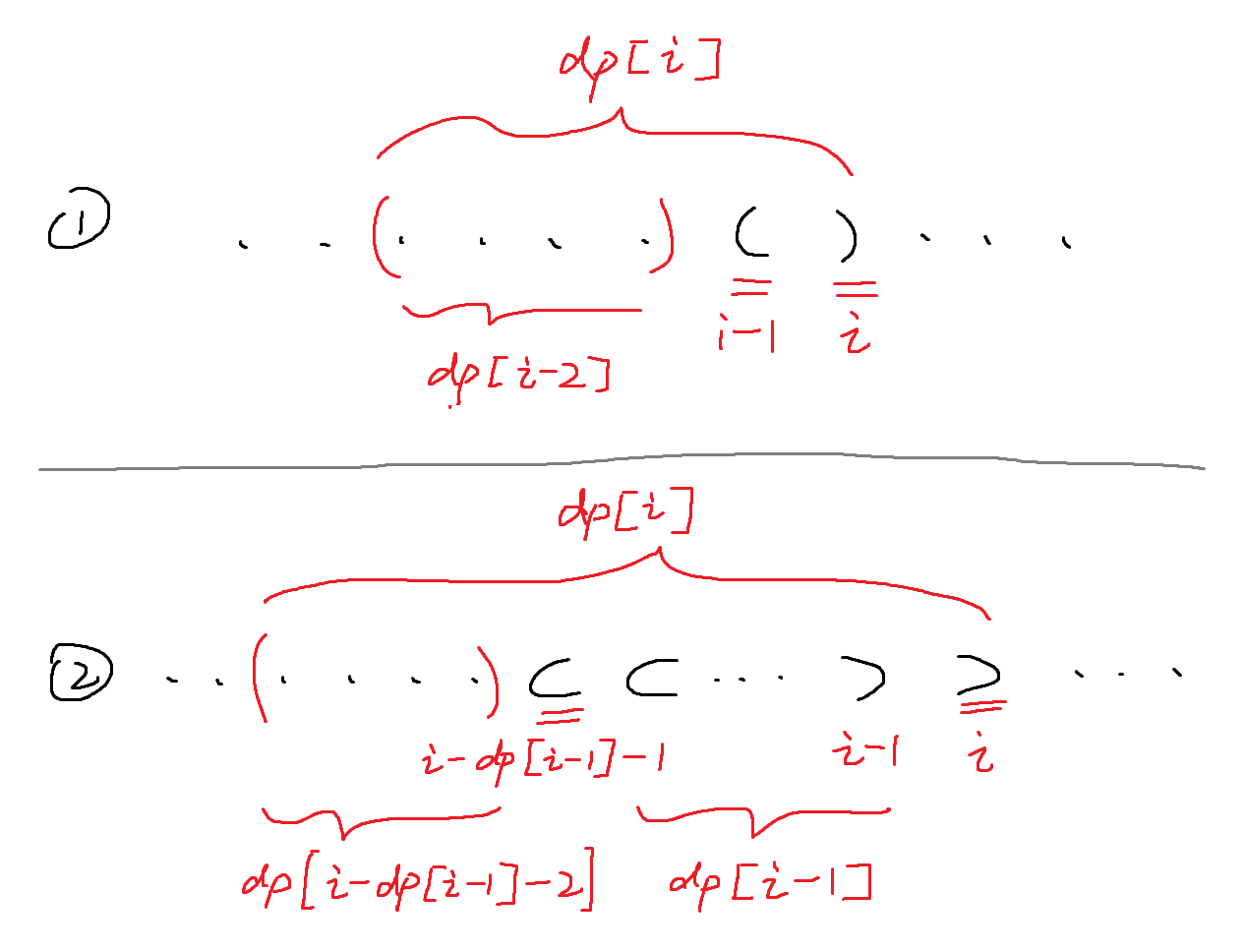
   

   public int longestValidParentheses(String s) {
    int len = s.length();
    if (len == 0) return 0;
   
    int max = 0;
   
    int[] dp = new int[len];
    dp[0] = 0;
   
    for (int i = 1; i < len; i++) {
        if (s.charAt(i) == ')') {
            if (s.charAt(i - 1) == '(') {
                dp[i] = 2 + (i > 1 ? dp[i - 2] : 0);
            } else if (i - dp[i - 1] - 1 >= 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                int prev = i - dp[i - 1] - 2;
                dp[i] = dp[i - 1] + 2 + (prev > 0 ? dp[prev] : 0);
            }
            max = Math.max(max, dp[i]);
        }
    }
    
    return max;
   }

300. 最长递增子序列

问题描述：找出整数数组 nums 中最长严格递增子序列（可不连续但按序）的长度。

• 示例 1：输入：[0,1,0,3,2,3] 输出：4（即 [0,1,2,3]）
• 示例 2：输入：[7,7,7,7,7,7,7] 输出：1 （即 [7]）

思路：定义 dp[i] 表示以下标 i 的整数结尾的子序列最长长度。

• 状态转移方程：dp[i] = max{dp[j]} + 1，其中 0 < j < i, nums[j] > nums[i] ；若所有 nums[j] 都大于 nums[i] ，则 dp[i] = 1。
• 初始值：dp[0] = 1 。

public int lengthOfLIS(int[] nums) {
    int len = nums.length;
    int[] dp = new int[len];
    Arrays.fill(dp, 1);

    for (int i = 1; i < len; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }

    int max = 0;
    for (int v : dp) {
        max = Math.max(max, v);
    }
    return max;
}