
先挖个坑,之后再填。。
目录
- B Tree & B+ Tree
- 红黑树(Red Black Tree)
- 哈希表 (Hash Table)
- 跳表(SkipList)
- 整数集合(IntSet)
- 压缩列表(ZipList)
- 快速列表(QuickList)
- 紧凑列表(ListPack)
- 布隆过滤器(BloomFilter)
B Tree & B+ Tree
......
红黑树(Red Black Tree)
......
哈希表(Hash Table)
......
跳表(SkipList)
思想:在单链表上增加多级索引(空间换时间)。地铁快慢线?(bushi)
时间复杂度:O(log N);空间复杂度:O(n) ;插入/删除时间复杂度:O(log N) 。
下图中,如果要找到值为 17 的结点,单链表需要遍历10个结点,而跳表仅需遍历7个。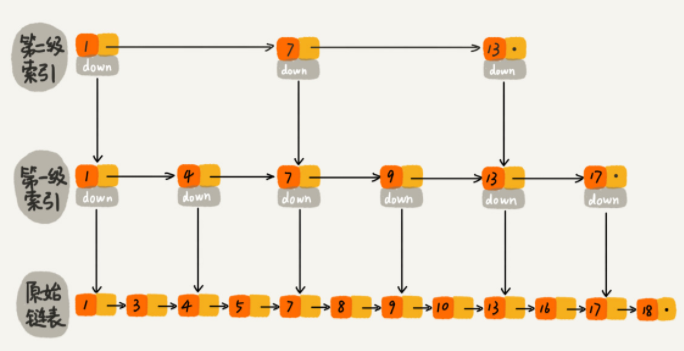
如下图所示,假如我们要查找的数据是 x ,在第 k 级索引中,我们遍历到 y 结点之后,发现 y < x < z ,所以我们通过 y 的down指针下降到第 k-1 级索引。在第 k-1 级索引中,y 和 z 之间只有3个结点,故每一级索引最多只需要遍历3个结点。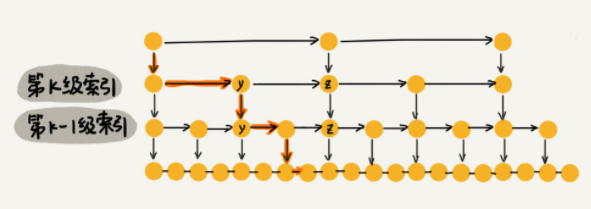
索引动态更新:当我们不断地往跳表中插入数据时,我们如果不更新索引,就有可能出现某两个索引节点间数据非常多的情况,极端情况下,跳表还会退化成单链表,如: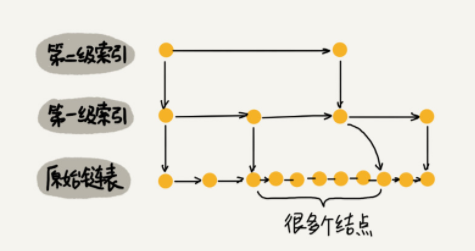
因此,当我们往跳表中插入数据的时候,我们可以通过一个随机函数生成值 K ,来决定这个结点添加到第一级到第 K 级的索引中:
Redis中Zset的实现:由 zskiplist(保存跳跃表节点的相关信息)和 zskiplistNode(表示跳跃节点)定义。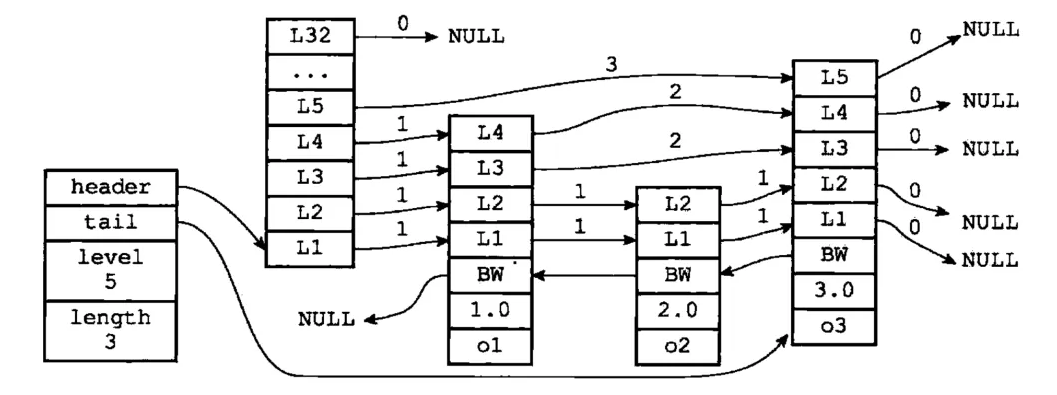
zskiplist 包含以下属性:
header:指向跳跃表的表头节点。tail:指向跳跃表的表尾节点。level:层数最大的节点层数(不含表头节点)。length:目前包含节点的数量(不含表头节点)。
zskiplistNode 包含以下属性:
level:L1代表第一层,L2代表第二层,以此类推。每个层都带有两个属性:前进指针和跨度。前进指针用于访问位于表尾方向的其它节点,而跨度则记录了前进指针所指向节点和当前节点的距离。BW:后退(backward)指针,指向当前节点的前一个节点,在程序从表尾向表头遍历时使用。score:各节点保存的分值,节点默认按分值升序排列。obj:节点所保存的成员对象(实际开发中,索引节点无需存储完整对象)。
Redis为什么用跳表而不用平衡树?
- 内存占用:平衡树每个节点包含
2个指针(指向左右子树),而跳表每个节点平均包含1/(1-p)个指针,Redis中取p=1/4,即1.33个指针。 - 范围查找:平衡树中找到指定范围的小值之后,还需要以中序遍历的顺序继续寻找其它不超过大值的节点;跳表只需要在找到小值之后,进行若干步的遍历即可。
- 实现简单:平衡树的插入和删除可能会引发子树的调整;跳表仅需修改相邻节点指针。
- 内存友好:B+ 树的设计目标是优化磁盘 I/O,通过减少树的高度来降低磁盘寻道次数,而 Redis 是内存数据库。
整数集合(IntSet)
整数集合本质上也是一块连续内存空间。当新加入的元素类型( int32_t )比整数集合现有所有元素的类型( int16_t )都要长时,整数集合需要先自动升级,按新元素的类型扩展 contents 数组的空间大小,然后才能将新元素加入到整数集合里,升级的过程中也要维持整数集合的有序性。
压缩列表(ZipList)
压缩列表是由连续内存块组成的顺序型数据结构,类似于数组。不仅可以利用CPU缓存,而且会针对不同长度的数据,进行相应编码,能够有效节省内存开销。
- 不能保存过多的元素,否则查询效率就会降低(从头遍历到尾)。
- 元素数量增加或长度发生变化时,内存空间需要重新分配,可能引发连锁更新的问题。因此仅用于节点数量不多的场景,只要数量足够小,即使发生连锁更新也能接受。
快速列表(QuickList)
快速列表其实就是双向链表 + 压缩列表组合:QuickList 是一个链表,链表中的每个元素又是一个压缩列表。通过控制每个链表节点中的压缩列表大小或元素个数,来减少连锁更新带来的影响,从而提供了更好的访问性能。
紧凑列表(ListPack)
紧凑列表不再像压缩列表一样记录前一个节点长度的字段,只记录当前节点的长度。当向 ListPack 加入新元素时,不会影响其他节点的长度字段的变化,从而避免了连锁更新。
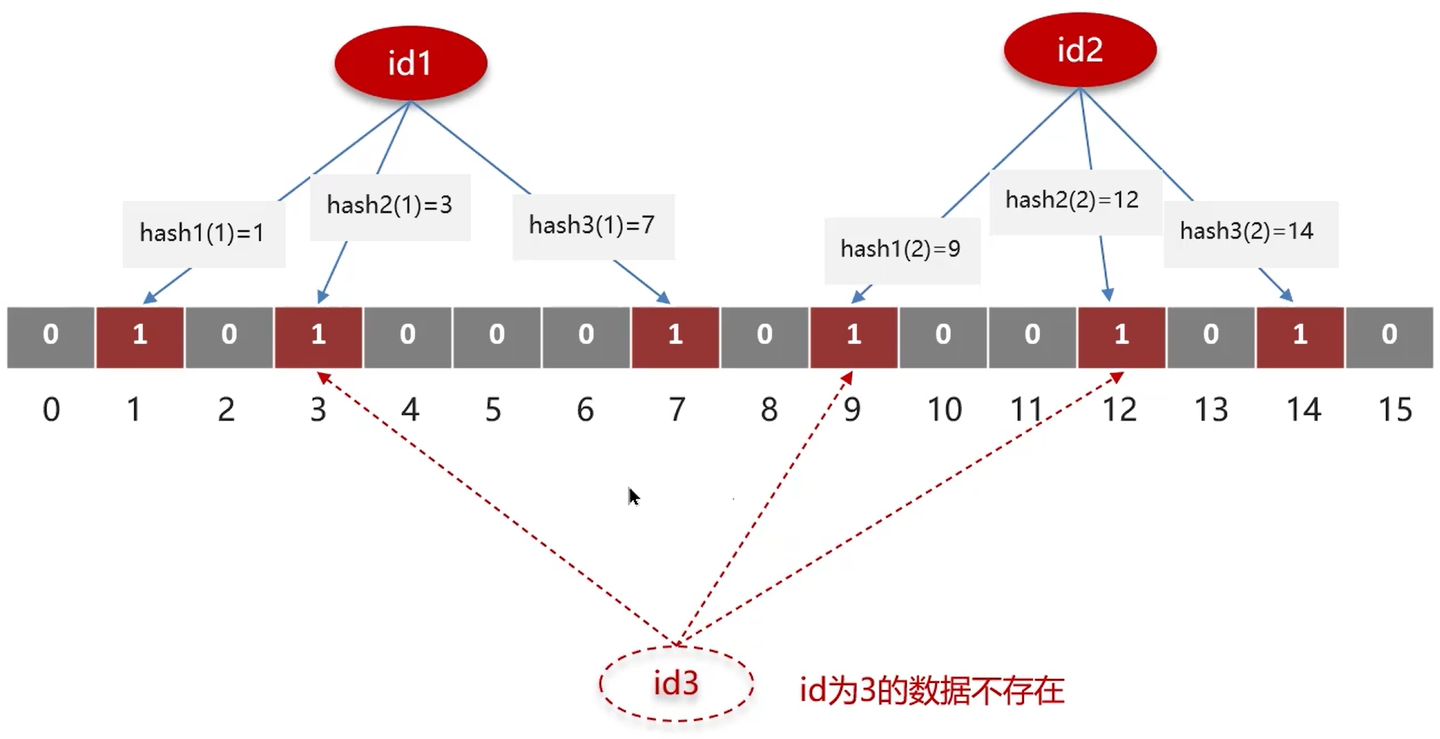
布隆过滤器(BloomFilter)
文章标题:一些数据结构
文章作者:nek0peko
文章链接:https://nek0peko.com/index.php/archives/2/
商业转载请联系站长获得授权,非商业转载请注明本文出处及文章链接,未经站长允许不得对文章文字内容进行修改演绎。
本文采用创作共用保留署名-非商业-禁止演绎4.0国际许可证